As I started to think about our next unit in math–factors and prime and composite numbers–I knew I wanted to dig into the concept of multiplication using an array model. I took one of my favorite lessons from recent years and tweaked it–and I needed it to be “sub-friendly” as I was going to be out of my classroom for training. Here’s how things all turned out!
The Task:
Students should be told that they are working at a factory that packages square chocolates. They have been asked to help the packaging department figure out all the different-sized boxes they need to package different amounts of chocolate. Because it is easiest to stack and ship rectangular boxes, chocolates can only be arranged into rectangular (arrays) boxes.
The goal is for students to understand that certain numbers have MANY different ways for the chocolates to be arranged. Conversely, others have only one way. I wanted to make sure students started in a very concrete way, so we actually wanted to BUILD the arrays. Here are the steps I recommend.
Building Arrays
Model the concept of the array with students. Make sure they are clear that an array is rectangular. I cannot lie. I love using a certain type of square, foil wrapped chocolates to show the concept of arrays. This is particularly powerful motivation—as the students can each eat part of the modeled array when they finish the lesson for the day! Consider a “medium sized” array to start—perhaps 12 candies. This allows them to see arrays of different shapes and sizes.
Next, show the students how arrays can face in different directions but are really worth the same amount. I also show the students how to use manipulatives to model this. You can use 1 inch tiles or even cut paper tiles–brown paper tiles can look an awful lot like chocolate if you use your imagination!
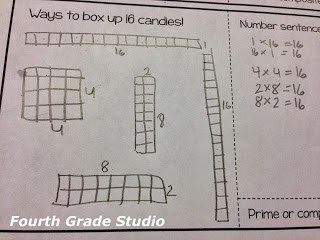
Drawing Representations
3. Model how students can sketch the arrays they build on the left side of their work space and write the coordinating number sentences on the right. Tell them to skip the “prime” and “composite” part for now. You decide if you want them to write BOTH numbers sentences (1 x 3= 3 AND 3 x 1 = 3) or if you only want them to write one of them.
4. After you have done the first few number combinations with the class, you can send them off to work more independently. I ask students to come and show me their work after they reach 12
chocolates so I can catch misconceptions. I do ask students to use the tiles or paper squares to show their modeling before drawing up to the point where I “release” them. Some students will need to continue to model throughout the activity. Others have a strong sense of multiplication and area and can derive all the possible combinations without a pictorial
representation.
chocolates so I can catch misconceptions. I do ask students to use the tiles or paper squares to show their modeling before drawing up to the point where I “release” them. Some students will need to continue to model throughout the activity. Others have a strong sense of multiplication and area and can derive all the possible combinations without a pictorial
representation.
NOTE: Some students struggle to find some of the “middle” arrays. They can see the long, skinny ones but struggle with the others. One prompt I offer is “Can you build a box that has 2 rows? How about 3?” and see if they can move from there.
Primes and Composite Numbers Day 2!
5. On day 2 of this investigation, revisit the array you made on day one with the wrapped chocolates. Introduce the term “factor” as you rebuild (using candies, tiles, paper squares, or sketches) all the possible arrays you can for that number. I show the students how to identify all the numbers that are “factors”. For example, for the number 12, students should have found:
1 x 12 = 12, 2 x 6 = 12, 3 x 4 = 12, 4 x 3 = 12, 6 x 2 = 12, 12 x 1= 12
6. I then show how I find ALL the different numbers that can be multiplied to make 12 and I circle them on the list. I have marked them in red to show this. Students quickly see that the “turn around fact” is simply the factors doubled. In this example, twelve has SIX factors.
1 x 12 = 12, 2 x 6 = 12, 3 x 4 = 12, 4 x 3 = 12, 6 x 2 = 12, 12 x 1 = 12
Finally!
7. The final step of this lesson sequence is to define prime and composite numbers. One of the easiest definitions for students this age to understand is the following:
●A prime number is a whole number GREATER THAN ONE which has exactly two factors—”one” and itself.
●A composite number is a whole number GREATER THAN ONE which can be divided by itself, one, and at least one other number.
Finally, help with prime and composite numbers!
I wrote everything down and got everything organized. I thought it might be something that others could use as well so I turned it into ready-to-use lesson for all of you! Click the image below or RIGHT HERE to see more about this great lesson for teaching prime and composite numbers!
Want to see more?
This blog post all about finding prime numbers shows the final part of this exploration in action!
Thanks for stopping by!