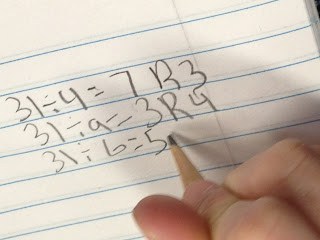We continued our division studies by reading and sharing the following book:
If you aren’t familiar with it, it is a cute tale that follows an insect “army” as they try to parade before the queen. They have 25 soldiers, and no matter how many rows they make, poor Joe always ends up a remainder which displeased her royal highness! Fortunately–the book DOES have a happy ending!
I read it aloud to my students and then asked them to write in their notebooks about what “math” they found in the book. This was a little tricky for them–they are getting better at explaining their OWN math, but it was hard for them to explain what they heard in the text.
So I decided to expand the task by trying it in a different way. I really wanted to build the students understanding that multiplication and division are “best friends”, so I showed the students a pile of 47 Hershey’s Kisses. (Note: There were 58 in the bag. You “do the math” about what you think happened . . .)
I told the students that I wanted to do the same thing as the insect army did–I wanted them to see what would happen if we “grouped” our candies in different ways. I reviewed how we would write that as an equation and sent them off to work. Many of the students dug right into it, but I sat back and watched for students who couldn’t get going numerically or who didn’t take the initiative to get up and get counters to model it.
After observing for a few minutes, I invited students who needed a “boost” to come work with me on the floor and we began to model with the candies themselves.
 |
| Here we put them in 3 groups and set aside our leftovers… |
 |
| We practiced writing our answers as number sentences with remainders… |
Students started noticing things such as . . .
“The more groups we have, the less in each group!”
“I thought there was going to be a pattern with the remainders but it didn’t work.”
“How come the remainders are usually small numbers?”
Other students were working on their own . . . some using counters, others using reasoning.
When they finished, I had them reach into a bucket and grab a handful of counters and roll a die to pick the number of groups. Some students didn’t get this far . . . but that’s ok!
When we got to a good stopping point, we worked as a class to answer the most important questions of all:
If we have 47 chocolates and 22 students, how many will each get?
What should we do with the remainder?
(HINT: I was licking my chops and panting at this point)
So . . . another day in the caloric trenches of my classroom. My goal today? That students understand the concept that when we divide, we are really figuring out “groups of” problems. I am hoping this is setting the foundation for our next work–the “partial quotient” algorithm. Stay tuned!