If you are unfamiliar with the CRA model for learning math, read on!  Today’s post is all about helping our students acquire multiplication facts in a research-based way that will cement true understanding.  So often we push memorization–and that IS our EVENTUAL goal!  In order for us to get there, we need to slow down and build understanding from the ground up.

Concrete Modeling

In order for students to understand the concept of multiplication, it is important for them to “see” the groups.  In fact, I have found that using the terms “groups of” instead of “times” is so important in the early stages of multiplication acquisition.  When we use stories to show multiplicative thinking and use actual objects to model it–students start to grasp the idea of repeated addition that is so important to multiplication.

It is important to provide plenty of practice at this level and to give students different manipulatives for students to use.  From pennies to centimeter cubes to mini erasers to arrays, there is no shortage of materials that can be used to help students see these groups and to make the connection between “groups of” and repeated addition.

When building groups of objects, the next concrete “step” is to start to arrange them in arrays.  Have conversations about how being organized can save us time.  If we have an array that is three rows of four, students need to start to see that they could also count four rows of three.  This helps build the understanding of fact families and turnaround facts.  Would you rather count five groups of three or three groups of five?  These are super valuable conversations to have!  Watch for my multiplication freebie to try some of these ideas with YOUR students!

Representation

The representational phase of this model takes away the concrete objects but still allows students to “show” their understanding–possibly through sketches or tally marks or even writing numbers to show the groups.  One thing I have found to be true over and over is that some students struggle to transition from the concrete stage to the slightly more abstract “representation” phase. As teachers, we are often anxious to get students to the abstract level, even if we aren’t aware that we are rushing things.

A few tips!

• Consider bridging the gap by first building, then drawing a picture of what you built.  Use stamps or a quick “X” in circles to make a picture of what you built. To really make the tie, try putting addition symbols between the pictures.
• Once students can see that their counters can be “drawn”, you can then move from drawing one “X” for each item to writing the actual number in each circle.
• After this, consider just writing the numbers next to each other with addition signs between them.
• Once students see the connection, connect the addition number sentence to the multiplication number sentence.

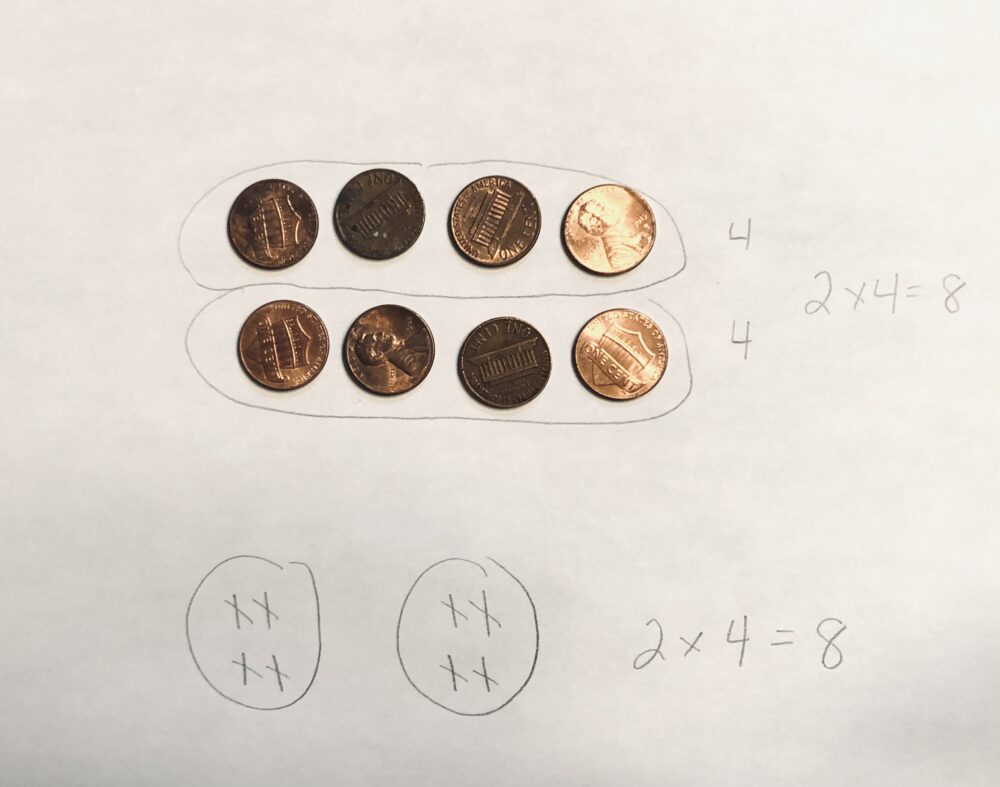
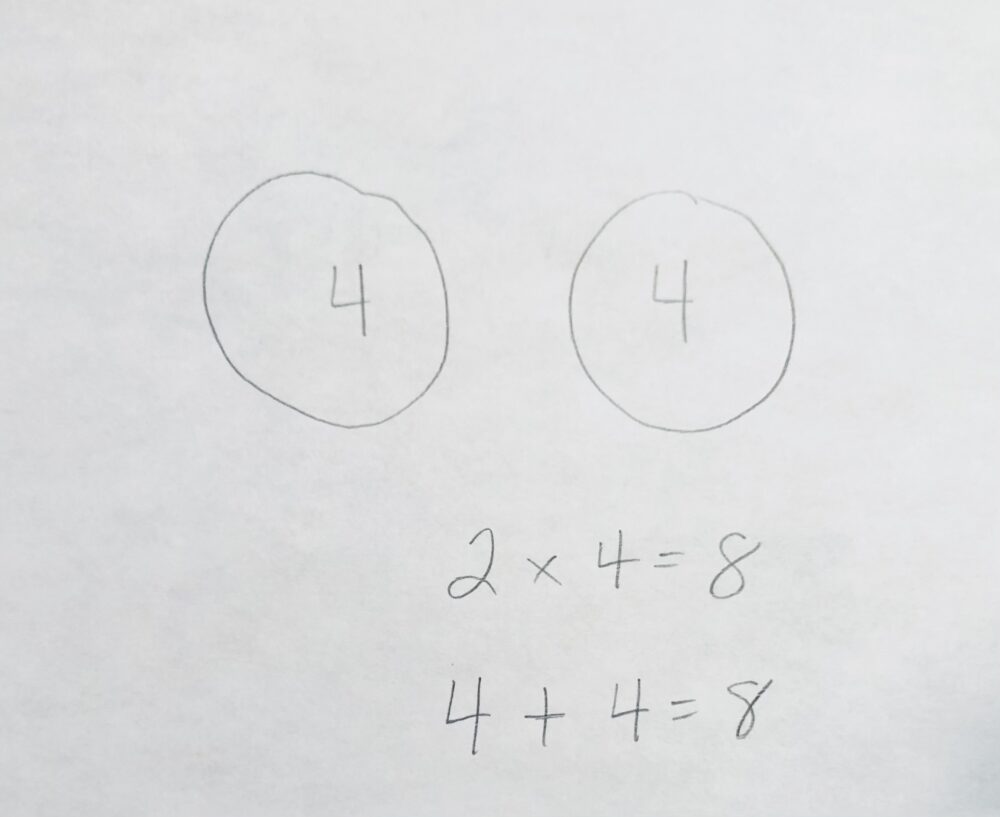
Abstract Understanding

During this phase, we move our students to the level where they use only numbers and symbols to represent their thinking.  Because of the work done earlier, now 3 x4 has a meaning.  We have told stories about three groups of four.  After that, we have built 3 groups of four counters.  Then we have drawn 3 groups of four.  We have skip counted groups of 4.  We have written the number 4 three times and have been able to compute the total.  At this point, students understand that 3 x 4 truly means “3 groups of 4” and do not need the support of something concrete to show it.

This is also a time to continue to look for patterns in multiplication facts.  What do we notice when we compare 2 x 4 and 4 x 4?  Refer back to those arrays we built and ask students to be detectives.  What do you notice?  Even displaying a multiplication table to study patterns is great–at THIS stage of development.  Don’t dig into this too soon!

Helping Students Acquire Multiplication Facts

If you would like to help students build that automaticity during the representational and abstract phases, I have created a set of games and activities that are designed to reinforce these strategies.  Remember, taking the time to build concrete models will go a LONG way to cementing those multiplication facts!  Helping students to acquire multiplication facts is so critical for the more advanced math that will face our students in upcoming years!

This toolkit has TONS of things for you to use to build these concepts…from sorting activities like this…

To using these premade “array builders” (so great for seeing “groups” of numbers for repeated adding!)  Literally building arrays using these dot strips of different amounts has helped SO many of my students experience those “oooooohhhh!” moments!

Or these skip counting practice cards…

To tons of games and other fluency practice activities!

CLICK HERE or the image below to see ALL that you get!  I seriously use the lessons and activities in this toolkit all year–from whole-class lessons to small group interventions to independent practice.  The games are perfect for math rotations or even to send home, and the other activities are meant to really help coach TRUE understanding of what multiplication is.

Multiplication fact fluency

Fluency comes from understanding patterns–and patterns develop when we “see” connections.  Building groups, modeling with arrays, gradually moving to representation, and then FINALLY to the more abstract is a slow but critical process.  Taking the time to build the foundations will pay off–I promise!  There’s even a FREEBIE sampler of this if you are interested–just CLICK HERE to grab it!

I wish you well!