As we have settled into some of our math routines, I have decided to really focus in on getting my students to have a bank of strategies to use when approaching a novel problem. I still have a fair number of students who look at a problem, sit back, and declare, “I don’t get it.” before even giving it a go.
Today’s “hints” involved trying the following steps:
1. Read the problem all the way through at least 2 times . . . the first time to make sure you know all the words, and the second time to try to “visualize” what is happening. For example, are you putting things together? Are items being sorted into boxes? Is something being eaten? Are you measuring?
2. Once students have read it twice, I suggested they highlight information that they feel is critical to the problem and then CIRCLE the actual question they are trying to answer. Now mind you…these are suggestions–I would never REQUIRE students to use these steps…they simply aren’t always needed! Teaching them is just meant to give students tools to add to their problem solving toolbox.

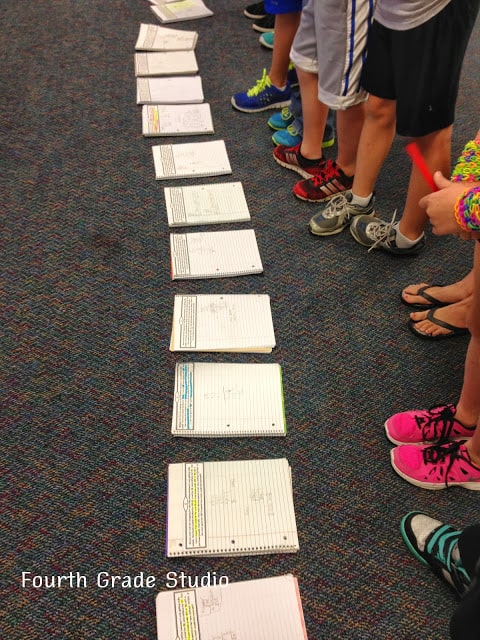
I heard a few more “OHHHHHHHHHHH!” sounds at this point, so I was pleased to see a few more students jump in and begin to work the problem. As I walked around asking questions and asking for explanations, I noticed an extreme lack of organization! Students were claiming to be finished, but I couldn’t tell where their answers were. There were two parts to this problem, and I couldn’t tell which answer was which–or even if both parts were complete. I kept my thoughts to myself for a while and then asked this group (My class was split into a group of 15 and a group of 9 today–each working on different things) to each bring their notebooks up and to put them in a row–no names on their pages.
I asked them to take a “gallery walk” and to be ready to discuss what they noticed about notebook pages that impressed them. After a few minutes, I asked them to go stand by one of the pages they wished to talk about.
I then asked them to talk about what they felt was most impressive about the problems they stood by, and I heard things like . . .
“The numbers are written so neatly.”
“The answer was easy to find.”
“It used the blue lines on the page.”
“This one had an explanation.”
and so on.
So . . . the students (and some of my TOP math students) were left realizing that getting a correct answer might not be enough! Tomorrow we are going to try again, and I hope that I will see a shift in both a willingness to “attack” the problem AND in their effort to organize their work. Baby steps, right? Happy Wednesday, everyone!
Are you interested in some of the problems shown in this post? Click the image below to take you to one of many similar sets in my store.