How many of you introduce the equal sign in the very first days of school? How often do you explore and study its role in math equations?

Algebraic Thinking in Elementary School? YES!
One thing that I have discovered over the years is that students can be very trained to “fill in the box”. The more focus we put on our math series and workbooks, the more true this is. In my mind, it is our obligation as elementary math teachers to develop mathematical thinking in our classrooms–and there are so many ways to nurture this…providing students with many rigorous problem-solving opportunities, having in-depth mathematical discussions, doing number talks, providing many different experiences to build numbers sense–and developing algebra thinking in our students.
What does the equal sign mean?
In a nutshell, algebra is the area of math that deals with mathematical symbols and the rules that exist for using them. As students get more sophisticated with their thinking, of course these symbols and rules get more complex. For me, one of the key symbols we can address in the intermediate grades is the equal sign.
The concept of “equals” is such an essential mathematical concept—and one that is often not taught explicitly in many math programs. Consider the following problem:
7 + 5 = ___ + 3
Students who have a good sense of the concept of equals know that “9” goes in the box. Every year, I am shocked by the number of students who think it is “12”—or that the problem can’t be solved at all! Many students are programmed to think that the “=“ sign means “find the answer” when, in actuality, it is a sign indicating that the two sides balance.
Deep understanding of this helps down the road with algebra and other more advanced math—and also makes a smooth transition to INequalities as well. Moving our “box” (or “variable”, or a letter, or a line, or a question mark) to different places in equations helps students think about numbers and equality and not just filling in the blank. So–give it a try!
See where your students are!
After we have a pretty in-depth discussion about this problem, we do a few more similar ones together and then I send my students off in pairs to try a BUNCH more–where they come up with the answer and must defend it by explaining the math. I want them using language like “In order to make the equation balance, both sides must be worth 13.
The right side already is, and the left side needs 6 more to make 13.” or something like that! The equal sign is so important. Students need to understand its role.
I walk around and monitor and coach this. Note, I really play this up. I explain that they are doing ALGEBRA and they love it! I tell them that we can make these problems more and more challenging as the year goes on–and we do!
Because we are working with whole numbers right now, I continue to have my students working on this “concept of equals” with harder and harder problems. Some of my students are even ready for an enrichment group where we learn about order of operations so we can solve some really fun ones!
As the year progresses, we can even do similar problems with decimals, fractions, measurement concepts and more!
Algebra thinking for math intervention? Focus on the equal sign
For some of my students, they need a little reinforcement with this. I met with a group to do more of the single digit cards where we broke out some manipulatives to model the balance. I have even pulled out a pan balance in the past to REALLY show this idea of “balance”. With intervention, it’s always smart to make things as concrete as possible Using counters or objects is always the best place to start.
Once my students started getting more confidence, I used this “The Missing Piece” game to start to expand the concept to double-digit numbers so students really see how “two parts” can make a “whole”. Even my stronger students love this game because they start to make some predictions about numbers they “need”–it’s fun to watch their growing mathematical thinking.
Even more algebraic thinking challenges!
Another great way to get student thinking algebraically is to provide students with problems where they have to “play” with numbers a little…like these “balance”-type problems. Again, our students are SO used to filling in the blanks that this type of problem is a great way to get students thinking in new ways. Instead of asking “What is 1 + 7?” or even “What are all the ways to make 8?”, these ask students to guess and check and keep multiple numbers in their minds.
They need to figure out what numbers go in each “bubble” to make the sum on the little bubbles true for ALL three (or four on some cards) true. This gets students really thinking about how numbers compose and decompose–so important! Once students start to think more flexibly, I start to do this type of problem with larger numbers. Click HERE or the image below to see more.
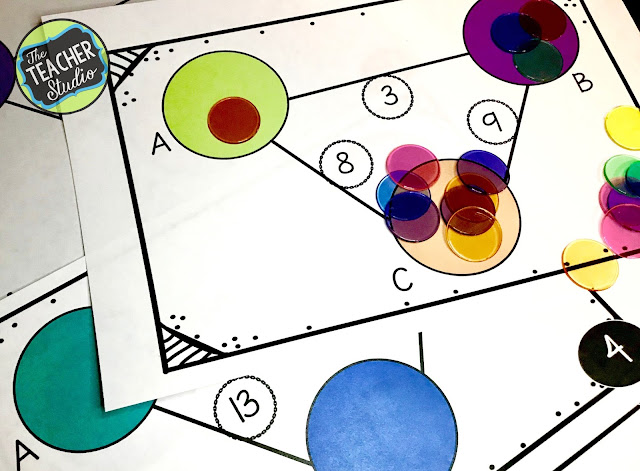
Another way to get students thinking algebraically is by extending the students’ work with “equal” and reasoning by using balanced mobile problems. These extend my students’ thinking about equal, about “halving”, and other key number sense concepts. I should really write a blog post about them because I LOVE the lessons that come out…from perseverance to “making sense of problems” to modeling with math–and more. I did make a little video with a few details…
How can I help?
So–I’d LOVE for you to try some of these ideas with your students and then let me know how it goes! If you want a set of task cards that have a whole bunch of problems like the ones at the top of the post (at 4 levels), just click the image below to see what I have been using with my students. Enjoy–and make sure to tell me what you find! If you are interested in the other resources, just click the images.
Interested in “The Missing Piece”? It’s one of the five addition and subtraction games in this resource:
Here’s another algebraic thinking post you might want to check out1
Want to pin this for later? Here you go!






